How To Find Inverse Of Absolute Value Function
ane.6: Absolute Value Functions
- Page ID
- 1298
Learning Objectives
- Graph an absolute value part.
- Solve an accented value equation.
Until the 1920s, the and then-called screw nebulae were believed to be clouds of dust and gas in our ain galaxy, some tens of thousands of light years away. Then, astronomer Edwin Hubble proved that these objects are galaxies in their ain correct, at distances of millions of light years. Today, astronomers can notice galaxies that are billions of light years away. Distances in the universe tin be measured in all directions. Every bit such, information technology is useful to consider distance as an accented value function. In this section, we will investigate absolute value functions.

Understanding Absolute Value
Call back that in its basic form \(f(x)=|x|\), the absolute value function, is one of our toolkit functions. The absolute value office is commonly thought of as providing the distance the number is from zero on a number line. Algebraically, for any the input value is, the output is the value without regard to sign.
Absolute Value Function
The absolute value function can be divers as a piecewise function
\[f(x)=|x|= \begin{cases} x & \text{ if }ten{\geq}0 \\ -10 & \text{ if } x<0 \end{cases}\]
Example \(\PageIndex{one}\): Determine a Number within a Prescribed Altitude
Describe all values \(ten\) within or including a distance of four from the number v.
Solution
Nosotros want the distance between \(ten\) and five to be less than or equal to four. We tin draw a number line, such as the one in , to represent the status to be satisfied.

The altitude from \(x\) to 5 can exist represented using the accented value as \(|10−v|\). We want the values of \(x\) that satisfy the condition \(| x−5 |\leq4\).
Analysis
Note that
\[\begin{align*} -four&{\leq}10-v & 10-5&\leq4 \\[4pt] 1&{\leq}x & x&{\leq}9 \end{align*}\]
And then \(|ten−5|\leq4\) is equivalent to \(one{\leq}x\leq9\).
However, mathematicians mostly prefer accented value notation.
Exercise \(\PageIndex{1}\)
Draw all values \(x\) inside a distance of 3 from the number two.
- Respond
-
\(|x−2|\leq3\)
Example \(\PageIndex{2}\): Resistance of a Resistor
Electrical parts, such as resistors and capacitors, come with specified values of their operating parameters: resistance, capacitance, etc. However, due to imprecision in manufacturing, the actual values of these parameters vary somewhat from slice to slice, even when they are supposed to exist the same. The all-time that manufacturers can practice is to try to guarantee that the variations will stay within a specified range, often ±1%, ±five%, or ±10%.
Suppose nosotros have a resistor rated at 680 ohms, ±v%. Apply the accented value role to express the range of possible values of the bodily resistance.
Solution
v% of 680 ohms is 34 ohms. The absolute value of the departure between the actual and nominal resistance should not exceed the stated variability, so, with the resistance \(R\) in ohms,
\[|R−680|\leq34 \nonumber\]
Exercise \(\PageIndex{2}\)
Students who score within 20 points of fourscore will pass a test. Write this as a distance from 80 using absolute value notation.
- Respond
-
Using the variable \(p\) for passing, \(| p−80 |\leq20\)
Graphing an Absolute Value Office
The most pregnant feature of the absolute value graph is the corner point at which the graph changes management. This point is shown at the origin in Figure \(\PageIndex{3}\).

Effigy \(\PageIndex{3}\) shows the graph of \(y=2|x–3|+iv\). The graph of \(y=|10|\) has been shifted right 3 units, vertically stretched past a factor of two, and shifted upwardly 4 units. This ways that the corner point is located at \((3,iv)\) for this transformed function.

Example \(\PageIndex{3}\): Writing an Equation for an Absolute Value Function
Write an equation for the role graphed in Figure \(\PageIndex{five}\).
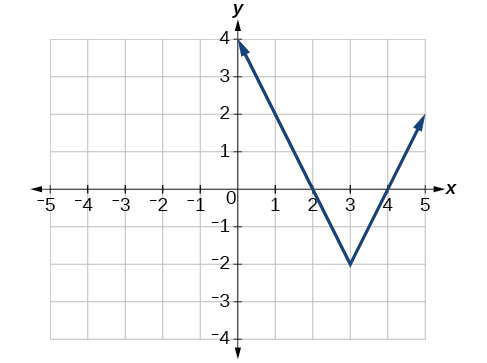
Solution
The bones absolute value part changes direction at the origin, then this graph has been shifted to the right three units and down ii units from the basic toolkit function. See Figure \(\PageIndex{vi}\).
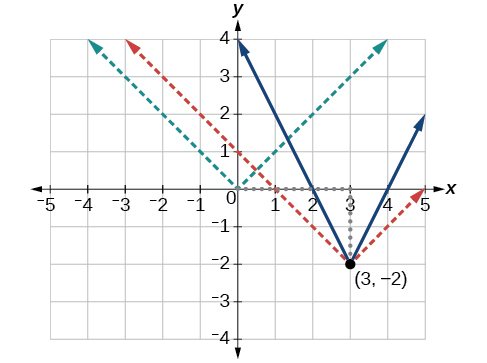
Nosotros also notice that the graph appears vertically stretched, because the width of the terminal graph on a horizontal line is not equal to 2 times the vertical distance from the corner to this line, as information technology would be for an unstretched absolute value function. Instead, the width is equal to 1 times the vertical distance every bit shown in Figure \(\PageIndex{7}\).
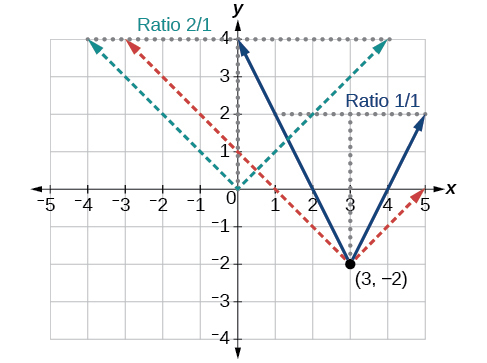
From this data we can write the equation
\[\begin{align*} f(x)&=two|10-3|-2, \;\;\;\;\;\; \text{treating the stretch equally a vertial stretch, or} \\ f(x)&=|ii(x-3)|-2, \;\;\; \text{treating the stretch as a horizontal pinch.} \finish{align*}\]
Analysis
Note that these equations are algebraically equivalent—the stretch for an accented value part can be written interchangeably equally a vertical or horizontal stretch or compression.
Q & A
If we couldn't detect the stretch of the part from the graphs, could we algebraically determine it?
- Answer
-
Yes. If nosotros are unable to determine the stretch based on the width of the graph, we can solve for the stretch factor by putting in a known pair of values for \(x\) and \(f(x)\).
\[f(x)=a|x−3|−ii \nonumber\]
At present substituting in the point \((ane, 2)\)
\[\brainstorm{align*} 2&=a|1-3|-2 \\ 4&=2a \\ a&=ii \end{align*}\]
Exercise \(\PageIndex{3}\)
Write the equation for the absolute value office that is horizontally shifted left ii units, is vertically flipped, and vertically shifted up 3 units.
- Answer
-
\(f(x)=−| ten+2 |+3\)
Q & A
Exercise the graphs of absolute value functions ever intersect the vertical axis? The horizontal centrality?
- Respond
-
Aye, they e'er intersect the vertical centrality. The graph of an absolute value function volition intersect the vertical axis when the input is goose egg.
No, they practise not always intersect the horizontal axis. The graph may or may non intersect the horizontal axis, depending on how the graph has been shifted and reflected. It is possible for the absolute value function to intersect the horizontal axis at zero, one, or 2 points (Figure \(\PageIndex{8}\)).
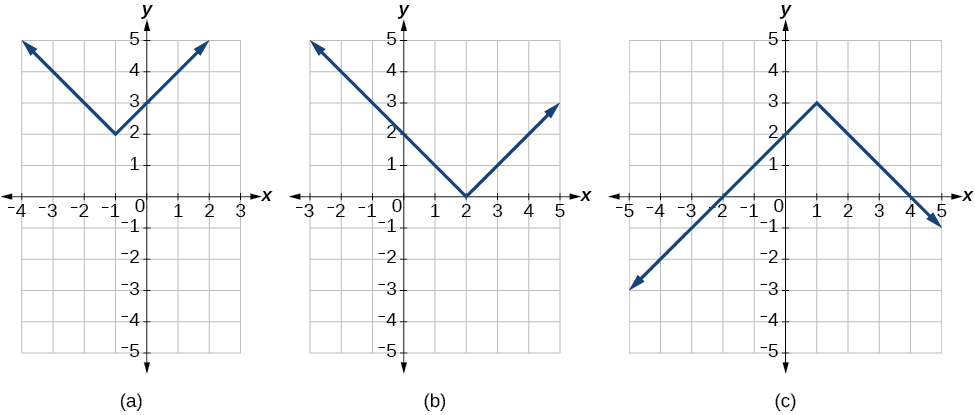
Figure \(\PageIndex{eight}\): (a) The accented value function does not intersect the horizontal axis. (b) The accented value function intersects the horizontal axis at one point. (c) The accented value function intersects the horizontal axis at two points.
Solving an Absolute Value Equation
Now that we can graph an absolute value office, we will learn how to solve an absolute value equation. To solve an equation such as \(eight=|2x−6|\), nosotros notice that the absolute value will exist equal to 8 if the quantity inside the absolute value is 8 or -8. This leads to ii different equations we tin can solve independently.
\[2x-six=8 \quad \text{ or } \quad 2x-6=-8 \nonumber\]
\[\begin{align*} 2x &= 14 & 2x &= -2 \\ x&=7 & 10&=-1 \end{align*}\]
Knowing how to solve problems involving absolute value functions is useful. For case, we may need to identify numbers or points on a line that are at a specified distance from a given reference betoken.
An accented value equation is an equation in which the unknown variable appears in absolute value bars. For example,
\[\begin{marshal*}|x|&=four, \nonumber \\[4pt] |2x−1| &=iii, \\[4pt] |5x+ii|−4 &=9. \end{marshal*}\]
Solutions to Absolute Value Equations
For existent numbers \(A\) and \(B\), an equation of the form \(|A|=B\), with \(B\geq0\), will have solutions when \(A=B\) or \(A=−B\). If \(B<0\), the equation \(|A|=B\) has no solution.
How To ...
Given the formula for an absolute value function, observe the horizontal intercepts of its graph.
- Isolate the absolute value term.
- Apply \(|A|=B\) to write \(A=B\) or \(−A=B\), bold \(B>0\).
- Solve for \(x\).
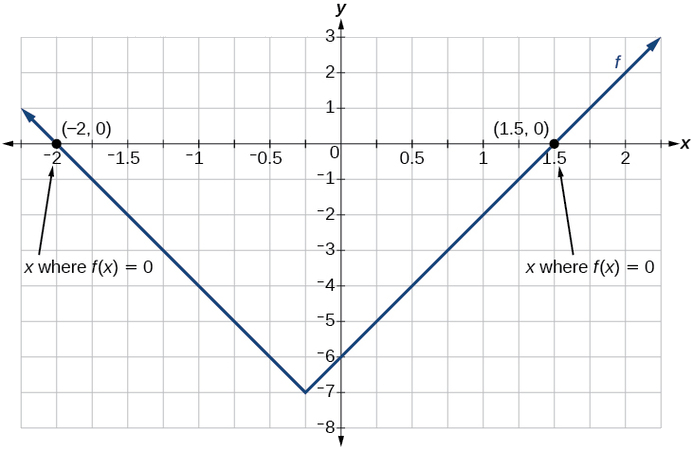
Example \(\PageIndex{4}\): Finding the Zeros of an Absolute Value Part
For the function \(f(10)=|4x+1|−7\), find the values of \(x\) such that \(f(10)=0\).
Solution
\[\brainstorm{align*} 0&=|4x+i|-seven & & &\text{Substitute 0 for f(ten).} \\ 7&=|4x+1| & & &\text{Isolate the absolute value on one side of the equation.} \\ 7&=4x+1 &\text{or} -7&=4x+1 &\text{Intermission into two split up equations and solve.} \\ 6&=4x & -8&=4x & \\ ten&=\frac{6}{4}=1.five & 10&=\frac{-8}{iv}=-2 \end{align*}\]
The office outputs 0 when \(x=one.5\) or \(x=−2\) (Figure \(\PageIndex{9}\)).
Exercise \(\PageIndex{four}\)
For the function \(f(x)=|2x−1|−iii\), find the values of \(x\) such that \(f(x)=0\).
Solution
\(x=−1\) or \(x=2\)
Q & A
Should nosotros ever look two answers when solving \(|A|=B\)?
Answer
No. We may find ane, two, or even no answers. For example, there is no solution to \(2+|3x−5|=i\).
How To ...
Given an absolute value equation, solve it.
- Isolate the absolute value term.
- Use \(|A|=B\) to write \(A=B\) or \(A=−B\).
- Solve for \(ten\).
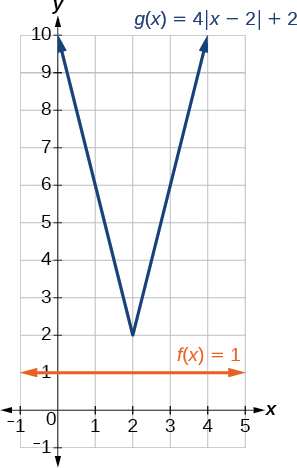
Example \(\PageIndex{5}\): Solving an Absolute Value Equation
Solve \(1=iv|x−ii|+ii\).
Solution
Isolating the absolute value on ane side of the equation gives the following.
\[\begin{align*} 1&=4|10-ii|+2 \\ -i&=4|x-2| \\ -\frac{ane}{4}&=|x-2| \end{align*}\]
The absolute value always returns a positive value, so it is incommunicable for the absolute value to equal a negative value. At this point, we notice that this equation has no solutions.
Q & A
In Example \(\PageIndex{v}\), if \(f(x)=i\) and \(thou(10)=4|10−2|+2\) were graphed on the same set of axes, would the graphs intersect?
Reply
No. The graphs of \(f\) and \(thousand\) would not intersect, as shown in Figure \(\PageIndex{10}\). This confirms, graphically, that the equation \(i=4|ten−two|+2\) has no solution.
Observe where the graph of the function \(f(x)=−| x+2 |+3\) intersects the horizontal and vertical axes.
\(f(0)=1\), and so the graph intersects the vertical axis at \((0,1)\). \(f(x)=0\) when \(x=−5\) and \(x=ane\) and so the graph intersects the horizontal axis at \((−5,0)\) and \((ane,0)\).
Solving an Absolute Value Inequality
Absolute value equations may not ever involve equalities. Instead, we may need to solve an equation inside a range of values. We would use an absolute value inequality to solve such an equation. An accented value inequality is an equation of the form
\[|A|<B,\;|A|{\leq}B,|A|>B, \nonumber\]
or
\[ |A|{\geq}B, \nonumber\]
where an expression \(A\) (and possibly but non usually \(B\)) depends on a variable \(x\). Solving the inequality means finding the fix of all \(ten\) that satisfy the inequality. Usually this prepare will be an interval or the union of two intervals.
At that place are two basic approaches to solving absolute value inequalities: graphical and algebraic. The advantage of the graphical approach is nosotros tin read the solution by interpreting the graphs of two functions. The advantage of the algebraic arroyo is it yields solutions that may be difficult to read from the graph.
For case, nosotros know that all numbers within 200 units of 0 may be expressed equally
\[|x|<200 \nonumber\]
or
\[ −200<10<200 \nonumber\]
Suppose nosotros desire to know all possible returns on an investment if we could earn some amount of money within $200 of $600. We tin solve algebraically for the prepare of values \(x\) such that the altitude betwixt \(x\) and 600 is less than 200. We represent the altitude between \(x\) and 600 as \(|x−600|\).
\[|10−600|<200\]
or
\[−200<x−600<200\]
\[\brainstorm{marshal*} −200+600< &x−600+600<200+600 \\[4pt] 400< &x<800 \cease{align*}\]
This means our returns would be between $400 and $800.
Sometimes an absolute value inequality problem volition exist presented to united states in terms of a shifted and/or stretched or compressed accented value function, where we must determine for which values of the input the function'southward output volition be negative or positive.
How To ...
Given an absolute value inequality of the course \(|x−A|{\leq}B\) for real numbers \(a\) and \(b\) where \(b\) is positive, solve the accented value inequality algebraically.
- Notice purlieus points by solving \(|ten−A|=B\).
- Test intervals created past the boundary points to make up one's mind where \(|ten−A|{\leq}B\).
- Write the interval or union of intervals satisfying the inequality in interval, inequality, or set-builder notation.
Example \(\PageIndex{6}\): Solving an Absolute Value Inequality
Solve \(|x −5|{\leq}iv\).
Solution
With both approaches, nosotros volition demand to know first where the corresponding equality is true. In this case nosotros first volition find where \(|x−5|=4\). We do this because the absolute value is a role with no breaks, so the merely style the function values tin can switch from being less than 4 to being greater than 4 is past passing through where the values equal 4. Solve \(|x−five|=iv\).
\[\brainstorm{align*} x−v&=4 &\text{ or }\;\;\;\;\;\;\;\; x&=9 \\ x−v&=−four & 10&=1\finish{marshal*}\]
After determining that the absolute value is equal to iv at \(x=i\) and \(x=9\), we know the graph tin can change but from being less than 4 to greater than 4 at these values. This divides the number line up into three intervals:
\[x<ane,\; 1<x<nine, \text{ and } x>nine. \nonumber\]
To determine when the function is less than 4, we could choose a value in each interval and run into if the output is less than or greater than 4, as shown in Table \(\PageIndex{1}\).
| Interval test \(ten\) | \(f(x)\) | \(<four\) or \(>4\) | |
|---|---|---|---|
| \(x<1\) | 0 | \(|0-5|=5\) | Greater than |
| \(i<x<9\) | 6 | \(|vi-5|=i\) | Less than |
| \(x>9\) | xi | \(|xi-5|=half dozen\) | Greater than |
Because \(1{\leq}x{\leq}9\) is the only interval in which the output at the test value is less than four, we tin can conclude that the solution to \(|10−5|{\leq}4\) is \(1{\leq}x{\leq}9\), or \([ane,ix]\).
To use a graph, nosotros can sketch the function \(f(x)=|x−5|\). To assistance us come across where the outputs are four, the line \(grand(x)=4\) could likewise be sketched as in Figure \(\PageIndex{11}\).
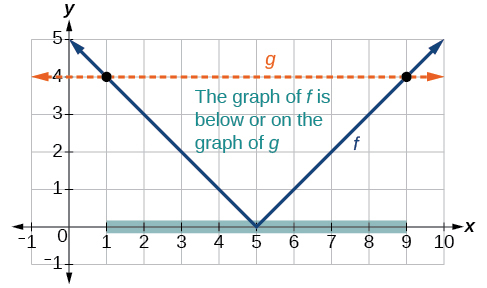
We can meet the following:
- The output values of the accented value are equal to iv at \(x=1\) and \(ten=9\).
- The graph of \(f\) is below the graph of \(g\) on \(1<x<ix\). This means the output values of \(f(ten)\) are less than the output values of \(g(x)\).
- The absolute value is less than or equal to 4 between these two points, when \(1{\leq}x\leq9\). In interval notation, this would exist the interval \([1,9]\).
Analysis
For absolute value inequalities,
\[|x−A|<C,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; |x−A|>C, \\−C<x−A<C,\;\;\;\; 10−A<−C \text{ or } x−A>C. \nonumber\]
The \(<\) or \(>\) symbol may be replaced by \(\leq\) or \(\geq\).
So, for this instance, we could utilise this alternative approach.
\[\begin{marshal*} |x−5|&{\leq}iv \\ −iv&{\leq}x−five{\leq}4 &\text{Rewrite by removing the accented value confined.} \\ −4+v&{\leq}x−5+5{\leq}four+5 &\text{Isolate the 10.} \\ i&{\leq}10\leq9 \terminate{align*}\]
Practice \(\PageIndex{five}\)
Solve \(|x+ii| \leq half dozen\).
- Respond
-
\(-8 \leq x \leq 4\)
How To ...
Given an absolute value function, solve for the ready of inputs where the output is positive (or negative).
- Set the function equal to zero, and solve for the boundary points of the solution set.
- Use test points or a graph to determine where the role's output is positive or negative.
Example \(\PageIndex{7}\): Using a Graphical Approach to Solve Absolute Value Inequalities
Given the function \(f(x)=−\frac{1}{2}|4x−5|+3\), determine the \(ten\)-values for which the office values are negative.
Solution
We are trying to make up one's mind where \(f(x)<0\), which is when \(−\frac{i}{ii}|4x−5|+3<0\). We brainstorm by isolating the absolute value.
\[ \brainstorm{align*} -\frac{1}{2}|4x−5|&<−3 \;\;\; \text{Multiply both sides by –2, and reverse the inequality.} \\ |4x−five|&>6\finish{align*}\]
Next we solve for the equality \(|4x−5|=half-dozen\).
\[\begin{align*} 4x-5&=6 & 4x-5&=-6 \\ 4x-6&=half-dozen \stop{marshal*}\]
or
\[\begin{align*} 4x&=-1 \\ x&=\frac{eleven}{iv} & 10&=-\frac{1}{four} \stop{align*}\]
Now, we tin examine the graph of \(f\) to discover where the output is negative. We will observe where the branches are beneath the \(ten\)-axis. Notice that it is non even important exactly what the graph looks similar, as long equally we know that it crosses the horizontal axis at \(10=−\frac{1}{iv}\) and \(x=\frac{11}{4}\) and that the graph has been reflected vertically. Encounter Figure \(\PageIndex{12}\).
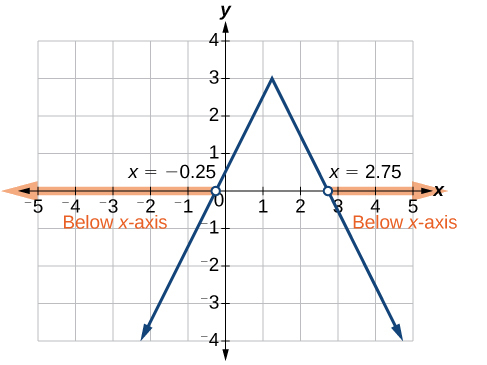
Nosotros observe that the graph of the function is beneath the \(ten\)-axis left of \(x=−\frac{i}{iv}\) and right of \(ten=\frac{eleven}{iv}\). This ways the office values are negative to the left of the first horizontal intercept at \(x=−\frac{i}{iv}\), and negative to the right of the second intercept at \(x=\frac{eleven}{iv} \). This gives the states the solution to the inequality.
\[x<−\frac{i}{four} \text{ or } 10>ane\frac{1}{4} \nonumber\]
In interval notation, this would be \(( −\infty,−0.25 )\cup( 2.75,\infty)\).
Exercise \(\PageIndex{6}\)
Solve \(−2|yard−4|\leq−half dozen\).
- Answer
-
\(k\leq1\) or \(k\geq7\); in interval notation, this would be \(\left(−\infty,1\right]\cup\left[seven,\infty\correct)\)
Central Concepts
- The absolute value function is commonly used to measure distances betwixt points.
- Applied problems, such every bit ranges of possible values, can too be solved using the accented value function.
- The graph of the accented value function resembles a letter 5. It has a corner point at which the graph changes management.
- In an absolute value equation, an unknown variable is the input of an absolute value function.
- If the absolute value of an expression is prepare equal to a positive number, expect two solutions for the unknown variable.
- An accented value equation may have one solution, two solutions, or no solutions.
- An accented value inequality is similar to an accented value equation but takes the form | A |<B, | A |≤B, | A |>B, or | A |≥B.It can be solved by determining the boundaries of the solution set up and so testing which segments are in the set.
- Absolute value inequalities tin can also be solved graphically.
Glossary
absolute value equation
an equation of the form \(|A|=B\), with \(B\geq0\); it will have solutions when \(A=B\) or \(A=−B\)
accented value inequality
a relationship in the grade \(|A|<B\), \(|A|{\leq}B\), \(|A|>B\), or \(|A|{\geq}B\)
Source: https://math.libretexts.org/Bookshelves/Precalculus/Precalculus_(OpenStax)/01%3A_Functions/1.06%3A_Absolute_Value_Functions
Posted by: hallettpasper.blogspot.com



0 Response to "How To Find Inverse Of Absolute Value Function"
Post a Comment