How To Find Angular Speed In Radians Per Second

How To Calculate The Angular Velocity Formula

Angular Velocity Formula: In physics,angular velocity refers to how fast an object rotates or revolves relative to another point, i.east. how fast the angular position or orientation of an object changes with fourth dimension. There are two types of angular velocity: orbital angular velocity and spin angular velocity. Spin angular velocity refers to how fast a rigid trunk rotates with respect to its center of rotation.

Orbital angular velocity refers to how fast a betoken object revolves about a fixed origin, i.e. the fourth dimension charge per unit of change of its angular position relative to the origin. In full general, angular velocity is measured in bending per unit time, eastward.g. radians per second. The SI unit of athwart velocity is expressed every bit radians/sec with the radian having a dimensionless value of unity, thus the SI units of athwart velocity are listed as1/sec. Angular velocity is usually represented past the symbol omega (ω, sometimesΩ). By convention, positive angular velocity indicates counter-clockwise rotation, while negative is clockwise.

For example, a geostationary satellite completes one orbit per mean solar day above the equator, or 360 degrees per 24 hours, and has athwart velocityω = 360 / 24 = 15 degrees per hr, or 2π / 24 ≈ 0.26 radians per hour. If bending is measured in radians, the linear velocity is the radius times the angular velocity, $v=r\omega$ . With orbital radius 42,000 km from the world's center, the satellite'south speed through space is thusv = 42,000 × 0.26 ≈ xi,000 km/60 minutes. The athwart velocity is positive since the satellite travels east with the Earth's rotation (counter-clockwise from to a higher place the north pole.)

How To Calculate The Angular Velocity Formula

In iii dimensions, angular velocity is a pseudovector, with its magnitude measuring the rate at which an object rotates or revolves, and its direction pointing perpendicular to the instantaneous plane of rotation or angular displacement. The orientation of athwart velocity is conventionally specified past the right-hand rule.

Formula For Angular Velocity

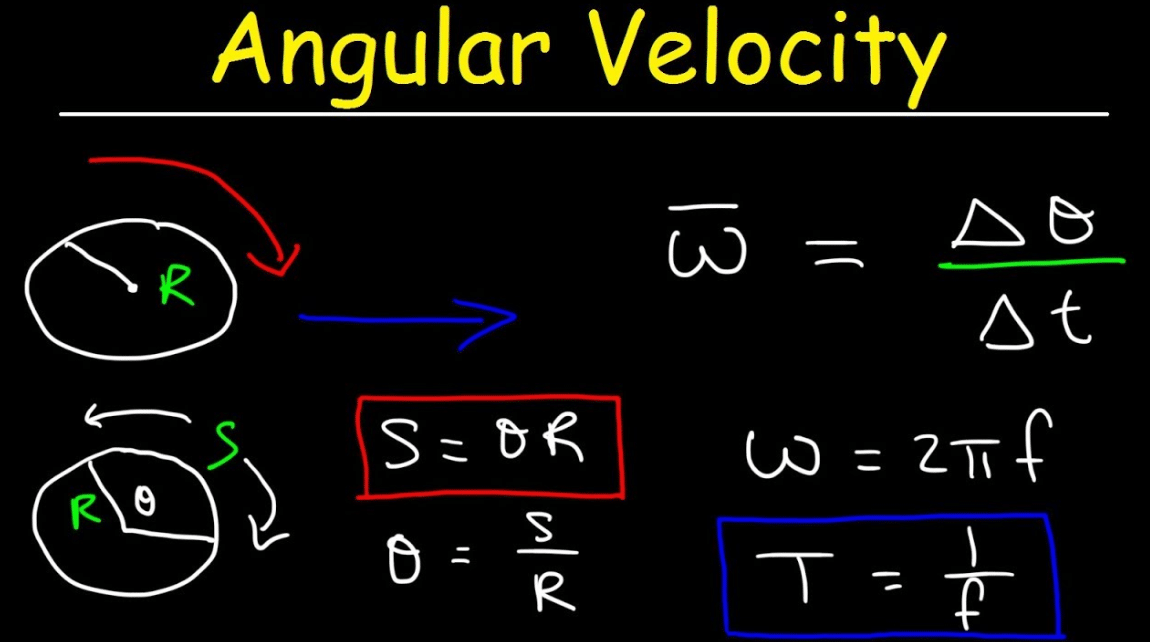
In the simplest instance of circular motion at radius $r$ , with position given by the angular displacement $\phi (t)$ from the ten-axis, the orbital angular velocity is the rate of change of angle with respect to time: $\omega ={\tfrac {d\phi }{dt}}$ . If $\phi$ is measured in radians, the distance from the 10-axis around the circle to the particle is $\ell =r\phi$ , and the linear velocity is $v(t)={\tfrac {d\ell }{dt}}=r\omega (t)$ , so that $\omega ={\tfrac {v}{r}}$ .

In the general case of a particle moving in the plane, the orbital angular velocity is the rate at which the position vector relative to a chosen origin "sweeps out" angle. The diagram shows the position vector $\mathbf {r}$ from the origin $O$ to a particle $P$ , with its polar coordinates $(r,\phi )$ . (All variables are functions of fourth dimension $t$ .) The particle has linear velocity splitting equally $\mathbf {v} =\mathbf {v} _{\|}+\mathbf {v} _{\perp }$ , with the radial component $\mathbf {v} _{\|}$ parallel to the radius, and the cross-radial (or tangential) component $\mathbf{v}_\perp$ perpendicular to the radius. When there is no radial component, the particle moves around the origin in a circumvolve; simply when there is no cross-radial component, it moves in a straight line from the origin. Since radial move leaves the angle unchanged, only the cross-radial component of linear velocity contributes to angular velocity.

The athwart velocityω is the rate of modify of athwart position with respect to time, which tin be computed from the cross-radial velocity every bit:

\omega ={\frac {d\phi }{dt}}={\frac {v_{\perp }}{r}}.

Here the cross-radial speed $v_\perp$ is the signed magnitude of $\mathbf{v}_\perp$ , positive for counter-clockwise motion, negative for clockwise. Taking polar coordinates for the linear velocity $\mathbf {v}$ gives magnitude $v$ (linear speed) and angle $\theta$ relative to the radius vector; in these terms, $v_{\perp }=v\sin(\theta )$ , then that

\omega ={\frac {v\sin(\theta )}{r}}.

These formulas may exist derived from $\mathbf {r} =(x(t),y(t))$ , $\mathbf {v} =(x'(t),y'(t))$ and $\phi =\arctan(y(t)/x(t))$ , together with the projection formula $v_{\perp }={\tfrac {\mathbf {r} ^{\perp }\!\!}{r}}\cdot \mathbf {v}$ , where $\mathbf {r} ^{\perp }=(-y,x)$ .

In 2 dimensions, angular velocity is a number with plus or minus sign indicating orientation, only not pointing in a direction. The sign is conventionally taken to exist positive if the radius vector turns counter-clockwise, and negative if clockwise. Angular velocity so may be termed a pseudoscalar, a numerical quantity which changes sign under a parity inversion, such every bit inverting ane centrality or switching the two axes.

Read Also: Perfect Square Trinomial Formula

Revolutions per minute can be converted toangular velocity in degrees per second by multiplying therpm past 6, since i revolution is 360 degrees and there are threescore seconds per minute. If therpm is irpm, theangular velocity in degrees per 2d would be 6 degrees per second, since 6 multiplied by 1 is 6.

To get our 2dformula for angular velocity, we recognize that theta is given in radians, and the definition of radian measure gives theta = southward / r. Thus, we can plug theta = s / r into our firstathwart velocity formula. This gives w = (southward / r) / t.

Angular velocity is the rotational speed. Something is spinning. It is an abridgement for Revolutions per infinitesimal. Other related units that express theaforementioned belongings are degrees per second and radians per 2nd.

Average Athwart Velocity Formula

First, when you are talking about "angular" annihilation, be it velocity or some other concrete quantity, recognize that, because you are dealing with angles, yous're talking about traveling in circles or portions thereof. You may remember from geometry or trigonometry that the circumference of a circle is its diameter times the constant pi, orπd. (The value of pi is nearly 3.14159.) This is more normally expressed in terms of the circumvolve's radiusr, which is half the diameter, making the circumference2πr.

In addition, yous have probably learned somewhere forth the mode that a circle consists of 360 degrees (360°). If you move a altitude Due south forth a circle, than the angular displacement θ is equal to South/r. I full revolution, then, gives 2πr/r, which merely leaves 2π. That means angles less than 360° can be expressed in terms of pi, or in other words, equally radians.

Taking all of these pieces of information together, you can express angles, or portions of a circle, in units other than degrees:

360° = (2π)radians, or

one radian = (360°/2π) = 57.three°,

Whereas linear velocity is expressed in length per unit of measurement time, angular velocity is measured in radians per unit time, usually per second.

If you know that a particle is moving in a circular path with a velocityv at a distancer from the center of the circle, with the direction of5 ever being perpendicular to the radius of the circle, and so the angular velocity tin be written

ω = v/r,

whereω is the Greek letter omega. Angular velocity units are radians per second; you tin too treat this unit of measurement every bit "reciprocal seconds," because five/r yields thousand/s divided by m, or s^-i, meaning that radians are technically a unitless quantity.

Centripetal Acceleration Formula Angular Velocity

The athwart dispatch formula is derived in the aforementioned essential way equally the athwart velocity formula: It is simply the linear acceleration in a direction perpendicular to a radius of the circumvolve (equivalently, its acceleration along a tangent to the circular path at any point) divided past the radius of the circumvolve or portion of a circle, which is:

α = a_t/r

This is also given by:

α = ω/t

because for circular motility, a_t = ωr/t = v/t.

α, equally you lot probably know, is the Greek letter "alpha." The subscript "t" here denotes "tangent."

Curiously enough, however, rotational motility boasts another kind of acceleration, called centripetal ("center-seeking") acceleration. This is given by the expression:

a_c = v²/r

This acceleration is directed toward the point around which the object in question is rotating. This may seem strange, since the object is getting no closer to this central point since the radiusr is fixed. Think of centripetal acceleration as a gratuitous-fall in which there is no danger of the object striking the ground, because the forcefulness drawing the object toward information technology (usually gravity) is exactly offset by the tangential (linear) acceleration described past the first equation in this section. Ifa_c were not equal toa_t , the object would either wing off into space or soon crash into the centre of the circle.

Read As well: Average and Instantaneous Rate of Change

Athwart Velocity Formula Physics

Earlier we can get to athwart velocity, we volition first review linear velocity.Linear velocity applies to an object or particle that is moving in a straight line. It is the rate of change of the object's position with respect to time.

Linear velocity can be calculated using the formula v =s /t, wherev = linear velocity,due south = altitude traveled, andt = time it takes to travel distance. For example, if I drove 120 miles in 2 hours, so to calculate my linear velocity, I'd plugsouthward = 120 miles, andt = ii hours into my linear velocity formula to getv = 120 / two = 60 miles per hour.One of the most common examples of linear velocity is your speed when you are driving down the road. Your speedometer gives your speed, or rate, in miles per hour. This is the rate of change of your position with respect to time, in other words, your speed is your linear velocity.

We take one more affair to review before getting to athwart velocity, and that is radians. When we deal with angular velocity, nosotros use the radian mensurate of an bending, so it is important that we are familiar with radian mensurate. The technical definition ofradian measure is the length of the arc subtended past the angle, divided by the radius of the circle the angle is a part of, where subtended ways to exist opposite of the angle and to extend from one indicate on the circle to the other, both marked off by the bending. This tells united states that an bending theta =s /r radians, wheres = length of the arc corresponding to theta, andr = radius of the circle theta is a part of.

Angular Velocity To Linear Velocity FormulaSince most of u.s. are comfortable with the degree measurement of angles, it is convenient that nosotros can easily catechumen caste measure to radian measure by multiplying the degree measure past pi / 180. For example, a 45 caste bending has a radian measure 45 (pi / 180), which is equal to pi / 4 radians.