how to find the sum of an infinite series

When the sum of an space geometric series exists, nosotros can summate the sum. The formula for the sum of an infinite series is related to the formula for the sum of the commencement [latex]north[/latex] terms of a geometric serial.

[latex]{South}_{n}=\frac{{a}_{1}\left(1-{r}^{n}\right)}{1-r}[/latex]

We will examine an infinite serial with [latex]r=\frac{1}{2}[/latex]. What happens to [latex]{r}^{n}[/latex] as [latex]north[/latex] increases?

[latex]\begin{assortment}{50}{\left(\frac{ane}{two}\correct)}^{ii}=\frac{1}{4}\\ {\left(\frac{1}{2}\right)}^{iii}=\frac{1}{eight}\\ {\left(\frac{1}{2}\right)}^{4}=\frac{1}{sixteen}\end{assortment}[/latex]

The value of [latex]{r}^{due north}[/latex] decreases rapidly. What happens for greater values of [latex]northward?[/latex]

[latex]\begin{array}{l}{\left(\frac{1}{2}\right)}^{10}=\frac{one}{1\text{,}024}\hfill \\ {\left(\frac{one}{2}\correct)}^{20}=\frac{ane}{1\text{,}048\text{,}576}\hfill \\ {\left(\frac{1}{two}\right)}^{30}=\frac{1}{1\text{,}073\text{,}741\text{,}824}\hfill \end{array}[/latex]

Every bit [latex]n[/latex] gets very large, [latex]{r}^{northward}[/latex] gets very small. We say that, as [latex]n[/latex] increases without jump, [latex]{r}^{northward}[/latex] approaches 0. As [latex]{r}^{n}[/latex] approaches 0, [latex]1-{r}^{n}[/latex] approaches 1. When this happens, the numerator approaches [latex]{a}_{one}[/latex]. This give us a formula for the sum of an infinite geometric serial.

A General Annotation: Formula for the Sum of an Infinite Geometric Series

The formula for the sum of an infinite geometric series with [latex]-1<r<i[/latex] is

[latex]S=\frac{{a}_{1}}{1-r}[/latex]

How To: Given an infinite geometric series, find its sum.

1. Identify [latex]{a}_{1}[/latex] and [latex]r[/latex].
2. Ostend that [latex]-i<r<1[/latex].
3. Substitute values for [latex]{a}_{1}[/latex] and [latex]r[/latex] into the formula, [latex]S=\frac{{a}_{1}}{ane-r}[/latex].
4. Simplify to find [latex]S[/latex].

Example seven: Finding the Sum of an Infinite Geometric Series

Find the sum, if it exists, for the post-obit:

1. [latex]x+9+8+7+\dots [/latex]
2. [latex]248.vi+99.44+39.776+\text{ }\dots [/latex]
3. [latex]\sum _{one thousand=ane}^{\infty }4\text{,}374\cdot {\left(-\frac{one}{3}\correct)}^{k - 1}[/latex]
4. [latex]\sum _{m=one}^{\infty }\frac{ane}{9}\cdot {\left(\frac{four}{iii}\right)}^{m}[/latex]

Solution

1. There is not a constant ratio; the series is not geometric.
2. In that location is a constant ratio; the series is geometric. [latex]{a}_{1}=248.half-dozen[/latex] and [latex]r=\frac{99.44}{248.half dozen}=0.4[/latex], so the sum exists. Substitute [latex]{a}_{1}=248.6[/latex] and [latex]r=0.iv[/latex] into the formula and simplify to find the sum:

   [latex]\begin{assortment}{l}Southward=\frac{{a}_{ane}}{i-r}\hfill \\ S=\frac{248.vi}{one - 0.iv}=414.\overline{3}\hfill \end{array}[/latex]

3. The formula is exponential, then the series is geometric with [latex]r=-\frac{one}{three}[/latex]. Detect [latex]{a}_{1}[/latex] by substituting [latex]one thousand=1[/latex] into the given explicit formula:

   [latex]{a}_{one}=4\text{,}374\cdot {\left(-\frac{1}{iii}\right)}^{one - one}=iv\text{,}374[/latex]

   Substitute [latex]{a}_{one}=iv\text{,}374[/latex] and [latex]r=-\frac{1}{3}[/latex] into the formula, and simplify to find the sum:

   [latex]\begin{array}{50}Southward=\frac{{a}_{one}}{1-r}\hfill \\ S=\frac{four\text{,}374}{1-\left(-\frac{1}{three}\right)}=iii\text{,}280.5\hfill \terminate{assortment}[/latex]

4. The formula is exponential, so the series is geometric, only [latex]r>1[/latex]. The sum does not exist.

Instance 8: Finding an Equivalent Fraction for a Repeating Decimal

Find an equivalent fraction for the repeating decimal [latex]0.\overline{3}[/latex]

Solution

We notice the repeating decimal [latex]0.\overline{three}=0.333..[/latex]. so we can rewrite the repeating decimal as a sum of terms.

[latex]0.\overline{three}=0.3+0.03+0.003+..[/latex].

Looking for a blueprint, we rewrite the sum, noticing that we see the showtime term multiplied to 0.1 in the 2d term, and the second term multiplied to 0.1 in the tertiary term.

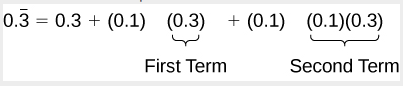
Notice the pattern; we multiply each consecutive term past a common ratio of 0.1 starting with the first term of 0.3. And so, substituting into our formula for an infinite geometric sum, we have

[latex]{S}_{n}=\frac{{a}_{1}}{1-r}=\frac{0.three}{i - 0.one}=\frac{0.3}{0.nine}=\frac{1}{3}[/latex].

Find the sum, if it exists.

Try It 12

[latex]ii+\frac{2}{3}+\frac{ii}{9}+..[/latex].

Solution

Try It 13

[latex]\sum _{k=1}^{\infty }0.76k+1[/latex]

Solution

Try It xiv

[latex]\sum _{k=i}^{\infty }{\left(-\frac{3}{eight}\right)}^{k}[/latex]

Solution

Source: https://courses.lumenlearning.com/ivytech-collegealgebra/chapter/finding-sums-of-infinite-series/

Posted by: hallettpasper.blogspot.com

Share this post